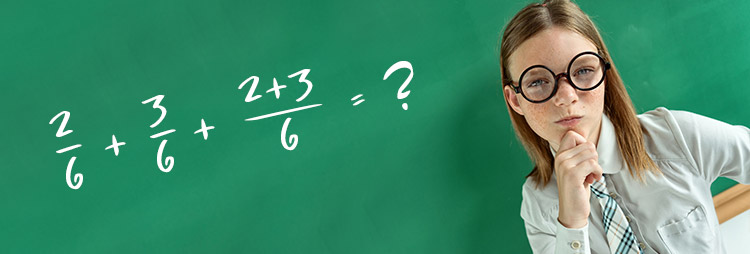Proszę Pani, a kiedy będą ułamki? To pytanie zna chyba każdy nauczyciel matematyki uczący czwartoklasistów. Naturalną ciekawość dzieci i ich chęć do pracy wystarczy tylko odpowiednio wykorzystać, aby obalić krążące legendy o problemach uczniów z ułamkami zwykłymi.
Pizze wycięte z kartonu i podzielone na kawałki różnej wielkości, krojenie jabłek, przelewanie wody z większych pojemników do mniejszych czy dzielenie szklanki na kilka części mazakiem – to "narzędzia" zazwyczaj w zupełności wystarczające, aby pokazać dzieciom, czym są ułamki zwykłe i jak wykonywać na nich działania.
Kiedy zapytamy dorosłych, gdzie dziecko będzie mogło zastosować ułamki zwykłe, następuje zwykle dłuższa chwila zastanowienia. I faktycznie – rozejrzyjmy się wokół… Liczby z przecinkami są wszędzie, ale ułamki zwykłe dzieci mogą spotkać chyba tylko w kuchennych przepisach i przy sprawiedliwym dzieleniu np. 3 kawałków ciasta między cztery osoby. Przecież nikt nigdy nie kupował 3/5 m tasiemki ani nie zastanawiał się, czy na słodycze wydał 2/7 czy może 5/8 swojego kieszonkowego. Do zrozumienia idei ułamków wystarczyłoby kilka lekcji matematyki. Zatem po co dziesięciolatkom ułamki zwykłe w takiej ilości, z jaką muszą się zmierzyć? Odpowiedź jest prosta. Ułamki zwykłe to baza do poznania ułamków dziesiętnych. Opanowanie podstawowych działań na ułamkach zwykłych jest więc konieczne, aby za jakiś czas zrozumieć i nawet polubić ułamki dziesiętne, towarzyszące nam na każdym kroku.
Dziwimy się często, że uczniowie nie pamiętają, jak się dodawało czy odejmowało ułamki zwykłe i co roku nauczyciele muszą powtarzać to samo. W tym nie ma nic dziwnego. Jak dziecko miało poćwiczyć nabyte umiejętności, skoro na co dzień nie było zbyt wielu okazji, a z ułamkami zwykłymi spotyka się głównie w szkole – na kilkunastu lekcjach w roku?
Już czwartoklasiści świetnie sobie radzą z dodawaniem i odejmowaniem ułamków – nie tylko o takich samych mianownikach, ale też o innych. Podobnie z porównywaniem ułamków. Dlaczego zatem przyjęło się, że porównywanie ułamków, w których ani liczniki, ani mianowniki nie są takie same dla ucznia 4 klasy jest za trudne? Po kilku przykładach dot. dodawania ułamków czy porównywania ułamków o takich samych mianownikach naturalnym jest zastanowić się, a co by było, gdyby mianowniki były inne. I dzieci same o to pytają! Mają przy tym sporo (często szalonych) pomysłów! Nie każmy im czekać na odpowiedź do piątej klasy, bo po pierwsze: to, że taką kolejność narzucił wybrany podręcznik, nie jest przecież wiążące, a po drugie – ich to ciekawi dziś, teraz i natychmiast chciałyby znać odpowiedź! Wykorzystajmy ich zaangażowanie i pomysłowość najpierw do dyskusji na poruszony temat, a potem do wyjaśnienia zagadnienia.
Lekcje dotyczące ułamków prawie wszystkim kojarzą się z nudnymi przykładami rachunkowymi wykonywanymi "od dzwonka do dzwonka". Oczywiście trening czyni mistrza, ale zamiana tablicy i kredy na inną, bardziej atrakcyjną dla dzieci formę sprawia, że zapominają one o tym, że lekcja dotyczy ułamków, a skupiają na "zastępnikach" w postaci kostek, kart, domin, gier planszowych, klamerek itp. Tutaj ograniczeniem jest tylko czas i pomysłowość nauczycieli.
Poniżej chciałam zaprezentować kilka takich właśnie zastępników, które urozmaicą lekcje dotyczące ułamków, będą pomysłem na lekcje powtórzeniowe bądź inspiracją do stworzenia własnych narzędzi pracy, pomogą również w powtórce ułamków w domu. W każdym z nich cel jest taki sam – zaprzyjaźnić się z ułamkami zwykłymi. Nawet jeżeli uczeń zrobi samodzielnie i ze zrozumieniem tylko dwa przykłady, to będą one cenniejsze niż kilkanaście zrobionych wspólnymi siłami na lekcji.
| Materiały do pobrania: | |
| Domino | Pobierz tutaj |
| Ćwiczenia z kostkami | Pobierz tutaj |
| Ćwiczenia z klamerkami | Pobierz tutaj |
| Ułamkowy Piotruś | Pobierz tutaj |
1) Domino
Klasyczne domino ze skracaniem i rozszerzaniem ułamków. Grupy (2 – 3 os.) rozsypują domino i próbują ułożyć z niego węża (w jednym kawałku). Wąż może też się zamknąć (głowa łączy się z ogonem). Uczniowie mają do dyspozycji kartki, na których mogą wykonywać obliczenia. Oceniamy poprawność, a nie czas wykonania zadania – aby wszyscy uczniowie mieli szansę na nagrodę w postaci oceny czy plusów z aktywności.
2) Krótkie podsumowania lekcji z kostkami
(odczytywanie ułamków, zamiana ułamków niewłaściwych na liczby mieszane, zamiana liczb mieszanych na ułamki niewłaściwe, porównywanie ułamków)
Na zakończenie lekcji dot. każdego z ww. zagadnień uczniowie otrzymują kostkę/kostki (najlepiej 10-ścienne) i jedną z kartek, na której znajdą instrukcję, co mają zrobić. Podsumowanie składa się z czterech rund. Po uzupełnieniu przez uczniów każdej z kartek zbieramy prace, sprawdzamy, czy punktacja wpisana przez uczniów się zgadza. Po ostatniej rundzie wystawiamy oceny. (Oczywiście to tylko jedna z możliwości).
3) Jenga z ułamkami
W Jengę grał każdy. Zasady standardowe, ale dodatkowo po każdym wyciągnięciu klocka uczeń wykonuje na kartce obliczenia przykładu, który wybrał. Na zakończenie zbieramy kartki i oceniamy poprawność. Warto zapowiedzieć na początku, że np. 3 osoby z klasy, które poprawnie obliczą największą liczbę przykładów, otrzymają szóstki. Najciekawsze jest to, że uczniom wcale nie przeszkadza, iż wykonują działania... Ich wersja jest taka, że po prostu grają w Jengę :)
A że klocki Jengi mają kilka stron, a na każdej można napisać przykłady, to jeden zestaw klocków można wykorzystać do kilku różnych tematów. (Moje Jengi mają z jednej strony dodawanie i odejmowanie ułamków zwykłych, z drugiej strony mnożenie i dzielenie ułamków dziesiętnych, a kolejne strony czekają na nowe pomysły).
4) Klamerki
Czteroosobowa grupa uczniów otrzymuje 20 klamerek. Ich zadaniem jest połączenie klamerek w pary. Można skracać ułamki, rozszerzać, zamieniać ułamki niewłaściwe na liczby mieszane albo odwrotnie – wszystkie poznane umiejętności mogą być zastosowane. Wystarczy nie zdradzać uczniom, czy powinny im zostać klamerki bez pary i oczywiście obiecać nagrodę za poprawne wykonanie zadania, aby usłyszeć dyskusje, wyjaśnienia, a nawet kłótnie z serii: To było inaczej, tak nie wolno, nie pamiętasz, to się robiło tak... itp.
5) Ułamkowy Piotruś
Propozycja na początkowe lekcje z zamiany ułamków niewłaściwych na liczby mieszane i odwrotnie. (Oczywiście modyfikacja wybranych ułamków może jeszcze uprościć albo utrudnić grę).
Na prawdziwe karty do gry naklejamy wydrukowane na samoprzylepnym papierze ułamki, tworząc 21 kart (10 par: ułamek niewłaściwy + odpowiadająca mu liczba mieszana oraz jeden "Piotruś"). Czteroosobowa grupa uczniów gra tak, jak w zwykłego Piotrusia. Uczniowie rozdają sobie karty. Zaczynają od znalezienia i wyłożenia na ławkę par, które znajdą wśród otrzymanych kart. (Wszyscy sprawdzają, czy wyłożone pary faktycznie są parami). Następnie uczniowie losują po kolei po jednej karcie od sąsiada. Chodzi o to, aby jak najszybciej wytypować, która karta jest Piotrusiem.
Zamiast bać się ułamków, bawmy się nimi!
Na podstawie przyniesionego przepisu na ciasto wyjaśnijmy, jak rozumieć zwroty półtorej szklanki mąki czy ćwierć kostki margaryny, przeliczmy ilość potrzebnych składników do upieczenia ciasta z 3/4 porcji. Przynieśmy 3 jabłka i nóż i poprośmy o rozdzielenie jabłek po równo między osiem osób. Pokażmy uczniom, że to, czego się uczą, można zastosować – to jest zawsze największy motywator do nauki. Oczywiście zanim przejdziemy do konkretów, musimy zadbać o teoretyczne przygotowanie naszych uczniów do rozwiązywania praktycznych problemów.
Pamiętajmy, że dzieci są ciekawe świata i nowości. Tyle czasu czekały na ułamki, nie pozwólmy, żeby się do nich zniechęciły!
Alicja Smolińska
Nauczycielka matematyki (od niedawna), działkowiczka (trochę dłużej), miłośniczka słodyczy (od zawsze). Na co dzień matematyczne zawiłości wyjaśnia na śliwkach, razem z uczniami zajadając czekoladę.